The capital asset pricing model – part 1

The cost of equity

Section E of the Study Guide for Financial Management contains several references to the Capital Asset Pricing Model (CAPM). This article introduces the CAPM and its components, shows how it can be used to estimate the cost of equity, and introduces the asset beta formula. Two further articles will look at applying the CAPM in calculating a project-specific discount rate, and will look at the theory, and the advantages and disadvantages of the CAPM.

Whenever an investment is made, for example in the shares of a company listed on a stock market, there is a risk that the actual return on the investment will be different from the expected return. Investors take the risk of an investment into account when deciding on the return they wish to receive for making the investment. The CAPM is a method of calculating the return required on an investment, based on an assessment of its risk.

Systematic and unsystematic risk

If an investor has a portfolio of investments in the shares of several different companies, it might be thought that the risk of the portfolio would be the average of the risks of the individual investments. In fact, it has been found that the risk of the portfolio is less than the average of the risks of the individual investments. By diversifying investments in a portfolio, therefore, an investor can reduce the overall level of risk faced.

There is a limit to this risk reduction effect, however, so that even a ‘fully diversified’ portfolio will not eliminate risk entirely. The risk which cannot be eliminated by portfolio diversification is called ‘undiversifiable risk’ or ‘systematic risk’, since it is the risk that is associated with the financial system. The risk which can be eliminated by portfolio diversification is called ‘diversifiable risk’, ‘unsystematic risk’, or ‘specific risk’, since it is the risk that is associated with individual companies and the shares they have issued. The sum of systematic risk and unsystematic risk is called total risk (Watson D and Head A, Corporate Finance: Principles and Practice, 7th edition, Pearson Education Limited, Harlow pp.245-6).

The capital and asset pricing model

The CAPM assumes that investors hold fully diversified portfolios. This means that investors are assumed by the CAPM to want a return on an investment based on its systematic risk alone, rather than on its total risk. The measure of risk used in the CAPM, which is called ‘beta’, is therefore a measure of systematic risk.

The minimum level of return required by investors occurs when the actual return is the same as the expected return, so that there is no risk of the investment’s return being different from the expected return. This minimum level of return is called the ‘risk-free rate of return’.

The formula for the CAPM, which is included in the formulae sheet, is as follows:

E(ri ) = Rf + βi(E(rm) – Rf)

E(ri) = return required on financial asset 

Rf = risk-free rate of return

βi = beta value for financial asset 

E(rm) = average return on the capital market

This formula expresses the required return on a financial asset as the sum of the risk-free rate of return and a risk premium – βi (E(rm) – Rf) – which compensates the investor for the systematic risk of the financial asset. If shares are being considered, E(rm) is the required return of equity investors, usually referred to as the ‘cost of equity’.

The formula is that of a straight line, y = a + bx, with βi as the independent variable, Rf as the intercept with the y axis, (E(r m ) – Rf) as the slope of the line, and E(ri) as the values being plotted on the straight line. The line itself is called the security market line (or SML), as shown in Figure 1.

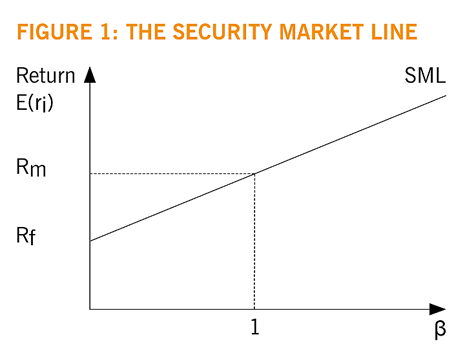
In order to use the CAPM, investors need to have values for the variables contained in the model.

The risk-free rate of return

In the real world, there is no such thing as a risk-free asset. Short-term government debt is a relatively safe investment, however, and in practice, it can be used as an acceptable substitute for the risk-free asset.

To ensure consistency of data, the yield on UK treasury bills is used as a substitute for the risk-free rate of return when applying the CAPM to shares that are traded on the UK capital market. Note that it is the yield on treasury bills which is used here, rather than the interest rate on treasury bills. The yield on treasury bills (sometimes called the yield to maturity) is the cost of debt of the treasury bills.

Because the CAPM is applied within a given financial system, the risk-free rate of return (the yield on short-term government debt) will change depending on which country’s capital market is being considered. The risk-free rate of return is also not fixed, but will change with changing economic circumstances.

The equity risk premium

Rather than finding the average return on the capital market, E(rm), research has concentrated on finding an appropriate value for (E(rm) – Rf), which is the difference between the average return on the capital market and the risk-free rate of return. This difference is called the equity risk premium, since it represents the additional return required for investing in equity (shares on the capital market as a whole) rather than investing in risk-free assets.

In the short term, share prices can fall as well as increase, so the average capital market return can be negative rather than positive. To smooth out short-term changes in the equity risk premium, a time-smoothed moving average analysis can be carried out over longer periods of time, often several decades. In the UK, when applying the CAPM to shares that are traded on the UK capital market, an equity risk premium of between 3.5% and 4.8% appears reasonable at the current time (Watson, D. and Head, A. (2016) Corporate Finance: Principles and Practice, 7th edition, Pearson Education Limited, Harlow p266).

Beta

Beta is an indirect measure which compares the systematic risk associated with a company’s shares with the systematic risk of the capital market as a whole. If the beta value of a company’s shares is 1, the systematic risk associated with the shares is the same as the systematic risk of the capital market as a whole.

Beta can also be described as ‘an index of responsiveness of the returns on a company’s shares compared to the returns on the market as a whole’. For example, if a share has a beta value of 1, the return on the share will increase by 10% if the return on the capital market as a whole increases by 10%. If a share has a beta value of 0.5, the return on the share will increase by 5% if the return on the capital market increases by 10%, and so on.

Beta values are found by using regression analysis to compare the returns on a share with the returns on the capital market. When applying the CAPM to shares that are traded on the UK capital market, beta values for UK companies can readily be found on the Internet, on Datastream, and from the London Business School Risk Management Service.

EXAMPLE 1

Calculating the cost of equity using the CAPM

Although the concepts of the CAPM can appear complex, the application of the model is straightforward. Consider the following information:

Risk-free rate of return = 4%

Equity risk premium = 5%

Beta value of Ram Co = 1.2

Using the CAPM:

E(ri) = Rf + βi (E(rm) – Rf) = 4 + (1.2 x 5) = 10%

The CAPM predicts that the cost of equity of Ram Co is 10%. The same answer would have been found if the information had given the return on the market as 9%, rather than giving the equity risk premium as 5%.

Asset betas, equity betas and debt betas

If a company has no debt, it has no financial risk and its beta value reflects business risk alone. The beta value of a company’s business operations as a whole is called the ‘asset beta’. As long as a company’s business operations, and hence its business risk, do not change, its asset beta remains constant.

When a company takes on debt, its gearing increases and financial risk is added to its business risk. The ordinary shareholders of the company face an increasing level of risk as gearing increases and the return they require from the company increases to compensate for the increasing risk. This means that the beta of the company’s shares, called the equity beta, increases as gearing increases (Watson, D. and Head, A. (2016) Corporate Finance: Principles and Practice, 7th edition, Pearson Education Limited, Harlow pp289-90).

However, if a company has no debt, its equity beta is the same as its asset beta. As a company gears up, the asset beta remains constant, even though the equity beta is increasing, because the asset beta is the weighted average of the equity beta and the beta of the company’s debt. The asset beta formula, which is included in the formulae sheet, is as follows:

Note from the formula that if Vd is zero because a company has no debt, βa = βe, as stated earlier.

EXAMPLE 2

Calculating the asset beta of a company

You have the following information relating to RD Co:

Equity beta of Tug Co = 1.2

Debt beta of Tug Co = 0.1

Market value of shares of Tug Co = $6m

Market value of debt of Tug Co = $1.5m

After tax market value of company = 6 + (1.5 x 0.75) = $7.125m

Company profit tax rate = 25% per year

β a = [(1.2 x 6)/7.125] + [(0.1 x 1.5 x 0.75)/7.125] = 1.024.

The next article will look at how the asset beta formula allows the CAPM to be applied in calculating a project-specific discount rate that can be used in investment appraisal.