Cost of capital, gearing and CAPM – part 1

Discounted cash flow techniques (DCFs), and in particular net present value (NPV), are generally accepted as the best ways of appraising projects. In DCF, future cash flows are discounted so that allowance is made for the time value of money. Two types of estimate are needed:

1. The future cash flows relevant to the project.
2. The discount rate to apply.

This article looks at how a suitable discount rate can be calculated.

The cost of equity

The cost of equity is the relationship between the amount of equity capital that can be raised and the rewards expected by shareholders in exchange for their capital. The cost of equity can be estimated in two ways: 

1. The dividend growth model
Measure the share price (capital that could be raised) and the dividends (rewards to shareholders). The dividend growth model can then be used to estimate the cost of equity, and this model can take into account the dividend growth rate. The formulae sheet for the Financial Management exam will give the following formulae:

P0 = D0(1 + g) / (re – g)

re = D0(1 + g) + g / P0

 

The first formula predicts the current ex-dividend market price of a share (P0) where:

D0 = the current dividend (whether just paid or just about to be paid)
g = the expected dividend future growth rate
re = the cost of equity.

Note that the top line (D0(1 + g)) is the dividend expected in one year’s time.

For a listed company, all the terms on the right of the equation are known, or can be estimated. In the absence of other data, the future dividend growth rate is assumed to continue at the recent historical growth rate. Example 1 sets out an example of how to calculate re.

Example 1
The dividend just about to be paid by a company is $0.24. The current market price of the share is $2.76 cum div. The historical dividend growth rate, which is expected to continue in the future, is 5%.

What is the estimated cost of capital?

Solution

re = D0(1 + g)/P0 + g = 0.24(1 + 0.05)/2.52 + 0.05 = 15%                          

P0 must be the ex-dividend market price, but we have been supplied with the cum-dividend price. The ex-dividend market price is calculated as the cum-dividend market price less the impending dividend. So here:

P0 = 2.76 – 0.24 = 2.52

The cost of equity is, therefore, given by:

re = D0(1 + g) / P0 + g

2. The capital asset pricing model (CAPM)
The capital asset pricing model (CAPM) equation quoted in the formula sheet is: E(ri) = Rf + ßi(E(rm) – Rf)

Where:
E(ri) = the return from the investment
Rf = the risk free rate of return
ßi = the beta value of the investment, a measure of the systematic risk of the investment
E(rm) = the return from the market

Essentially, the equation is saying that the required return depends on the risk of an investment. The starting point for the rate of return is the risk free rate (Rf), to which you need to add a premium relating to the risk. The size of that premium is determined by the answers to the following:

• What is the premium the market currently gives over the risk free rate (E(rm) – Rf)? This is a reference point for risk: how much does the stock market, as a whole, return in excess of the risk free rate?
• How risky is the specific investment compared to the market as a whole? This is the ‘beta’ of the investment (ßi). If ßi is 1, the investment has the same risk as the market overall. If ßi > 1, the investment is riskier (more volatile) than the market and investors should demand a higher return than the market return to compensate for the additional risk. If ßi < 1, the investment is less risky than the market and investors would be satisfied with a lower return than the market return.

Example 2
Risk free rate = 5%
Market return = 14%

What returns should be required from investments whose beta values are:
(i) 1
(ii) 2
(iii) 0.5

E(ri) = Rf +ßi(E(rm) – Rf)

(i) E(ri) = 5 + 1(14 – 5) = 14%
The return required from an investment with the same risk as the market, which is simply the market return.

(ii) E(ri) = 5 + 2(14 – 5) = 23%
The return required from an investment with twice the risk as the market. A higher return than that given by the market is therefore required.

(iii) E(ri) = 5 + 0.5(14 – 5) = 9.5%
The return required from an investment with half the risk as the market. A lower return than that given by the market is therefore required.

Comparing the dividend growth model and CAPM

The dividend growth model allows the cost of equity to be calculated using empirical values readily available for listed companies. Measure the dividends, estimate their growth (usually based on historical growth), and measure the market value of the share (though some care is needed as share values are often very volatile). Put these amounts into the formula and you have an estimate of the cost of equity.

However, the model gives no explanation as to why different shares have different costs of equity. Why might one share have a cost of equity of 15% and another of 20%? The reason that different shares have different rates of return is that they have different risks, but this is not made explicit by the dividend growth model. That model simply measures what’s there without offering an explanation. Note particularly that a business cannot alter its cost of equity by changing its dividends. The equation:

re = D0(1 + g) / P0 + g

might suggest that the rate of return would be lowered if the company reduced its dividends or the growth rate. That is not so. All that would happen is that a cut in dividends or dividend growth rate would cause the market value of the company to fall to a level where investors obtain the return they require.

The CAPM explains why different companies give different returns. It states that the required return is based on other returns available in the economy (the risk free and the market returns) and the systematic risk of the investment – its beta value. Not only does CAPM offer this explanation, it also offers ways of measuring the data needed. The risk free rate and market returns can be estimated from economic data. So too can the beta values of listed companies. It is, in fact, possible to buy books giving beta values and many investment websites quote investment betas.

When an investment and the market is in equilibrium, prices should have been adjusted and should have settled down so that the return predicted by CAPM is the same as the return that is measured by the dividend growth model.

Note also that both of these approaches give you the cost of equity. They do not give you the weighted average cost of capital other than in the very special circumstances when a company has only equity in its capital structure.

What contributes to the risk suffered by equity shareholders, hence contributing to the beta value?

There are two main components of the risk suffered by equity shareholders:

1. The nature of the business. Businesses that provide capital goods are expected to show relatively risky behaviour because capital expenditure can be deferred in a recession and these companies’ returns will therefore be volatile. You would expect ßi > 1 for such companies. On the other hand, a supermarket business might be expected to show less risk than average because people have to eat, even during recessions. You would expect ßi < 1 for such companies as they offer relatively stable returns.
2. The level of gearing. In an ungeared company (ie one without borrowing), there is a straight relationship between profits from operations and earnings available to shareholders. Once gearing, and therefore interest, is introduced, the amounts available to ordinary shareholders become more volatile. Look at Example 3 below.

Example 3: level of gearing

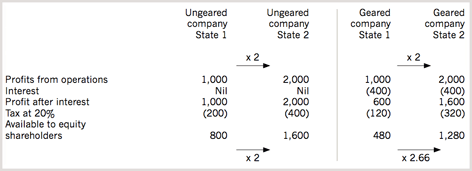
This shows two companies, one ungeared, one geared, which carry on exactly the same type of business. Between State 1 and State 2, their profits from operations double. The amounts available to equity shareholders in the ungeared company also double, so equity shareholders experience a risk or volatility which arises purely from the company’s operations. However, in the geared company, while amounts available from operations double, the amounts available to equity shareholders increase by a factor of 2.66. The risk faced by those shareholders therefore arises from two sources: risk inherent in the company’s operations, plus risk introduced by gearing.

Therefore, the rate of return required by shareholders (the cost of equity) will also be affected by two factors:

1. The nature of the company’s operations.
2. The amount of gearing in the company.

When we talk about, or calculate, the ‘cost of equity’ we have to be clear what we mean. Is this a cost which reflects only the business risk, or is it a cost which reflects the business risk plus the gearing risk?

When using the dividend growth model, you measure what you measure. In other words, if you use the dividends, dividend growth and share price of a company which has no gearing, you will inevitably measure the ungeared cost of equity. That’s what shareholders are happy with in this environment. If, however, these quantities are derived from a geared company, you will inevitably measure the geared company’s cost of equity.

Similarly, published beta values are derived from observing how specific equity returns vary as market returns vary, to see if a share’s return is more or less volatile than the market. Once again, you measure what you measure. If the company being observed has no gearing in it, the beta value obtained depends only on the type of business being carried on. If, however, the company has gearing within it, the beta value will reflect not only the risk arising from the company, but also the risk arising from gearing.