CAPM: theory, advantages, and disadvantages

Section E of the Financial Management study guide contains several references to the Capital Asset Pricing Model (CAPM). This article is the final one in a series of three, and looks at the theory, advantages, and disadvantages of the CAPM. The first article in the series introduced the CAPM and its components, showed how the model could be used to estimate the cost of equity, and introduced the asset beta formula. The second article looked at applying the CAPM in calculating a project-specific discount rate to use in investment appraisal.

CAPM formula

The linear relationship between the return required on an investment (whether in stock market securities or in business operations) and its systematic risk is represented by the CAPM formula, which is given in the Formulae Sheet:

The CAPM is an important area of financial management. In fact, it has even been suggested that financial management only became an academic discipline when William Sharpe published his derivation of the CAPM in 1964.

CAPM assumptions

The CAPM is often criticised as unrealistic because of the assumptions on which the model is based, so it is important to be aware of these assumptions and the reasons why they are criticised. The assumptions are as follows (Watson, D. and Head, A. (2016) Corporate Finance: Principles and Practice, 7th edition, Pearson Education Limited, Harlow pp.258-9).

Investors hold diversified portfolios

This assumption means that investors will only require a return for the systematic risk of their portfolios, since unsystematic risk has been diversified and can be ignored.

Single-period transaction horizon

A standardised holding period is assumed by the CAPM  to make the returns on different securities comparable. A return over six months, for example, cannot be compared to a return over 12 months. A holding period of one year is usually used.

Investors can borrow and lend at the risk-free rate of return

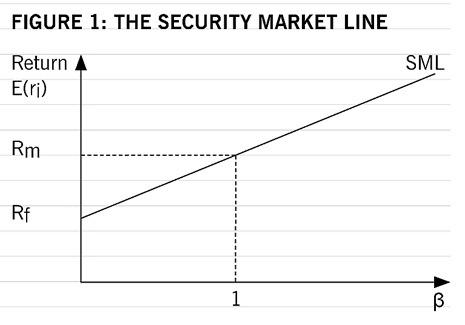
This is an assumption made by portfolio theory, from which the CAPM was developed, and provides a minimum level of return required by investors. The risk-free rate of return corresponds to the intersection of the security market line (SML) and the y-axis (see Figure 1). The SML is a graphical representation of the CAPM formula.

Perfect capital market

This assumption means that all securities are valued correctly and that their returns will plot on to the SML. A perfect capital market requires the following: that there are no taxes or transaction costs; that perfect information is freely available to all investors who, as a result, have the same expectations; that all investors are risk averse, rational and desire to maximise their own utility; and that there are a large number of buyers and sellers in the market.

While the assumptions made by the CAPM allow it to focus on the relationship between return and systematic risk, the idealised world created by the assumptions is not the same as the real world in which investment decisions are made by companies and individuals.

Real-world capital markets are clearly not perfect, for example. Even though it can be argued that well-developed stock markets do, in practice, exhibit a high degree of efficiency, there is scope for stock market securities to be priced incorrectly and so  for their returns not to plot onto the SML.

The assumption of a single-period transaction horizon appears reasonable from a real-world perspective, because even though many investors hold securities for much longer than one year, returns on securities are usually quoted on an annual basis.

The assumption that investors hold diversified portfolios means that all investors want to hold a portfolio that reflects the stock market as a whole. Although it is not possible to own the market portfolio itself, it is quite easy and inexpensive for investors to diversify away specific or unsystematic risk and to construct portfolios that ‘track’ the stock market. Assuming that investors are concerned only with receiving financial compensation for systematic risk seems therefore to be quite reasonable.

A more serious problem is that investors cannot in the real world borrow at the risk-free rate (for which the yield on short-dated government debt is taken as a proxy). The reason for this is that the risk associated with individual investors is much higher than that associated with the government. This inability to borrow at the risk-free rate means that in practice the slope of the SML is shallower than in theory.

Overall, it seems reasonable to conclude that while the assumptions of the CAPM represent an idealised world rather than the real-world, there is a strong possibility, in the real world, of a linear relationship between required return and systematic risk.

WACC and CAPM

The weighted average cost of capital (WACC) can be used as the discount rate in investment appraisal provided that some restrictive assumptions are met. These assumptions are as follows:

• the investment project is small compared to the investing organisation
• the business activities of the investment project are similar to the business activities currently undertaken by the investing organisation
• the financing mix used to undertake the investment project is similar to the current financing mix (or capital structure) of the investing company
• existing finance providers of the investing company do not change their required rates of return as a result of the investment project being undertaken.

These assumptions are essentially saying that WACC can be used as the discount rate provided that the investment project does not change either the business risk or the financial risk of the investing organisation.

If the business risk of the investment project is different to that of the investing organisation, the CAPM can be used to calculate a project-specific discount rate. The procedure for this calculation was covered in the second article in this series.

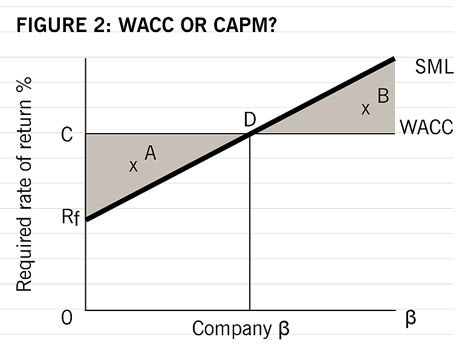
The benefit of using a CAPM-derived project-specific discount rate is illustrated in Figure 2. Using the CAPM will lead to better investment decisions than using the WACC in the two shaded areas, which can be represented by projects A and B.

Project A would be rejected if WACC is used as the discount rate, because the internal rate of return (IRR) of the project is less than the WACC. This investment decision is incorrect, however, since project A would be accepted if a CAPM-derived project-specific discount rate is used because the project IRR lies above the SML. The project offers a return greater than that needed to compensate for its level of systematic risk, and accepting it will increase the wealth of shareholders.

Project B would be accepted if WACC was used as the discount rate because its IRR is greater than the WACC.

This investment decision is also incorrect, however, since project B would be rejected if using a CAPM-derived project-specific discount rate, because the project IRR offers insufficient compensation for its level of systematic risk (Watson and Head, pp.291-2).

Advantages of the CAPM

The CAPM has several advantages over other methods of calculating required return, explaining why it has been popular for more than 40 years:

• It considers only systematic risk, reflecting a reality in which most investors have diversified portfolios from which unsystematic risk has been essentially eliminated.
• It is a theoretically-derived relationship between required return and systematic risk which has been subject to frequent empirical research and testing.
• It is generally seen as a much better method of calculating the cost of equity than the dividend growth model (DGM) in that it explicitly considers a company’s level of systematic risk relative to the stock market as a whole.
• It is clearly superior to the WACC in providing discount rates for use in investment appraisal.

Disadvantages of the CAPM

The CAPM suffers from several disadvantages and limitations that should be noted in a balanced discussion of this important theoretical model.

Assigning values to CAPM variables

To use the CAPM, values need to be assigned to the risk-free rate of return, the return on the market, or the equity risk premium (ERP), and the equity beta.

The yield on short-term government debt, which is used as a substitute for the risk-free rate of return, is not fixed but changes regularly with changing economic circumstances. A short-term average value can be used to smooth out this volatility.

Finding a value for the equity risk premium (ERP) is more difficult. The return on a stock market is the sum of the average capital gain and the average dividend yield. In the short term, a stock market can provide a negative rather than a positive return if the effect of falling share prices outweighs the dividend yield. It is therefore usual to use a long-term average value for the ERP, taken from empirical research, but it has been found that the ERP is not stable over time. In the UK, an ERP value of between 3.5% and 4.8% is currently seen as reasonable. However, uncertainty about the ERP value introduces uncertainty into the calculated value for the required return.

Beta values are now calculated and published regularly for all stock exchange-listed companies. The problem here is that uncertainty arises in the value of the expected return because the value of beta is not constant, but changes over time.

Using the CAPM in investment appraisal

Problems can arise in using the CAPM to calculate a project-specific discount rate. For example, one common difficulty is finding suitable proxy betas, since proxy companies very rarely undertake only one business activity. The proxy beta for a proposed investment project must be disentangled from the company’s equity beta. One way to do this is to treat the equity beta as a portfolio beta (βp), an average of the betas of several different areas of proxy company activity, weighted by the relative share of the proxy company market value arising from each activity.

βp = (W1β1) + (W2β2)

W1 and W2 are the market value weightings of each business area
β1 and β2 are the equity betas of each business area.

Example

A proxy company, Gib Co, has an equity beta of 1.2. Approximately 75% of the business operations of Gib Co by market value are in the same business area as a proposed investment. However, 25% of its business operations by market value are in a business area unrelated to the proposed investment. These unrelated business operations are 50% riskier, in systematic risk terms, than those of the proposed investment. What is proxy equity beta for the proposed investment?

Solution

Using the portfolio beta formula, βp = (W1β1) + (W2β2):

1.2 = (0.75 x β1) + (0.25 x 1.5 x β1) = (0.75 x β1) + (0.375 x β1) = 1.125 x β1

Proxy equity beta = β1 = 1.2/ 1.125 = 1.067

In this case note that β2 = 1.5 x β1

The information about relative shares of proxy company market value may be quite difficult to obtain.

A similar difficulty is that ungearing proxy company betas uses capital structure information that may not be readily available. Some companies have complex capital structures with many different sources of finance. Other companies may have untraded debt or use complex sources of finance such as convertible bonds.

The simplifying assumption that the beta of debt is zero will also lead to inaccuracy, however small,  in the calculated value of the project-specific discount rate.

Another disadvantage in using the CAPM in investment appraisal is that the assumption of a single-period time horizon is at odds with the multi-period nature of investment appraisal. While CAPM variables can be assumed constant in successive future periods, experience indicates that this is not true in the real world.

Conclusion

Research has shown the CAPM stands up well to criticism, although attacks against it have been increasing in recent years. Until something better presents itself, though, the CAPM remains a very useful item in the financial management toolkit.